COMPAS 업데이트 후 Optimap이 뭐만 하면 다운되서 만들어 봄
결국 VBA는 중고등학생 수준의 원시적인 코드만 사용하다 끝날 것 같다. 살기 위해 아둥바둥하며 배운게 다 그렇겠지만.
<컨셉>
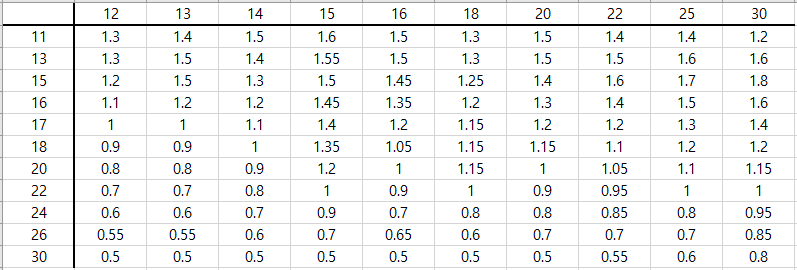
아래와 같은 테이블을 가정한다.

경향성 자체는 존재하지만 상당한 굴곡이 있다. 이 테이블을 인접한 영역의 데이터를 반영하여 적절히 펼치고자 한다.
예를 들어, x = 16 / y = 15에 대응되는 데이터는 아래의 주변 값들을 고려해 전체적인 경향성에 맞는 값으로 수정하는 것이다.

당연한 이야기지만 원 데이터와 가까울 수록 가중치를 크게 주고, 멀어질 수록 가중치를 적게 가져간다.
사실 가중치를 어떻게 가져가느냐가 관건인데, 딱히 아는 게 없어 그냥 정규분포 곡선을 이용하였다.
<코드 전문 (코드 원문 : 검정색, 설명 : 파란색)>
Sub smo2D()
'input
CalRange = 2
QFac = 1
ReDim ResBox(2 * CalRange * CalRange + 2 * CalRange, 1)
CalRange는 인접한 몇 셀 까지를 확인할 지를 결정한다. 2를 둘 경우 위의 그림과 같이 2셀 안의 데이터를 연산에 고려한다.
QFac은 정규분포에서 사용하는 Q factor이며, 1일 경우 표준정규분포를 만족한다.
- 이 부분들은 추후 Function화 시킬 때 입력 값으로 적절히 변경한다.
ResBox는 결과 도출을 위해 중간 결과들을 임시로 저장해 두는 배열 변수이다.
필요한 연산 결과의 수는 CalRange에 따른 계차수열이 되므로 이와 같이 정의.
'area determination
x0 = 2
y0 = 2
x_end = 11
y_end = 12
연산이 되는 셀의 주소를 고정해 두었다. 간편한 디버깅을 위함이며 이 부분 또한 추후 Function화 시킬 때 적절히 변경한다.
'range scailing x
xDif = 0
xCnt = 0
For i = x0 To x_end - 1
xDif = xDif + Cells(y0 - 1, i + 1) - Cells(y0 - 1, i)
xCnt = xCnt + 1
Next
xDifAvr = xDif / xCnt
'range scailing y
yDif = 0
yCnt = 0
For i = y0 To y_end - 1
yDif = yDif + Cells(i + 1, x0 - 1) - Cells(i, x0 - 1)
yCnt = yCnt + 1
Next
yDifAvr = yDif / yCnt
정규 분포 상의 단위와 각 축간 단위가 서로 다를 수 있으므로 일치시켜주는 작업.
위의 예시는 아니지만, rpm의 경우 보통 100 단위로 움직이고, 외기온의 경우는 약 5 단위로 움직인다. 이 경우, 온도의 1 단위 변화량은 rpm의 20 단위 변화량과 같다.
이를 처리하는 방법은 여러 가지가 있겠으나, 일단은 축 별로 값의 편차를 모두 구해 평균을 내고, 이렇게 계산된 평균적인 차이를 1로 스케일링한다.
'range determination
For ix = x0 To x_end
For iy = y0 To y_end
InputTmp = 0
For jx = -CalRange To CalRange
For jy = -CalRange To CalRange
If Abs(jx) + Abs(jy) <= CalRange Then
2D 테이블 안의 모든 셀에 대하여 연산을 진행하며(ix, iy), 개별 연산마다 CalRange에서 설정한 변수만큼의 인접한 셀을 확인한다. (jx, jy)
For문의 특성 상 아래 그림과 같이 +/-CalRange 셀을 모두 확인하는데, 정확히 2셀 안쪽 만큼 떨어진 부분만 확인하기 위해 jx + jy가 CalRange값보다 클 경우(회색 셀) 연산을 수행하지 않는다.

따라서 최종적으로, 노란색 셀 영역에서만 편차를 계산하여 결과에 반영하게 된다.
CaseXDet = ix - x0 + jx
CaseYDet = iy - y0 + jy
Select Case CaseXDet
Case Is < 0
If CaseYDet < 0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x0))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y0, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y0, x0)
ElseIf CaseYDet > y_end - y0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x0))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y_end, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y_end, x0)
Else
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x0))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(iy + jy, x0 - 1))) / yDifAvr
DataVal = Cells(iy + jy, x0)
End If
Case Is > x_end - x0
If CaseYDet < 0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x_end))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y0, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y0, x_end)
ElseIf CaseYDet > y_end - y0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x_end))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y_end, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y_end, x_end)
Else
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, x_end))) * 2 / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(iy + jy, x0 - 1))) / yDifAvr
DataVal = Cells(iy + jy, x_end)
End If
Case Else
If CaseYDet < 0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, ix + jx))) / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y0, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y0, ix + jx)
ElseIf CaseYDet > y_end - y0 Then
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, ix + jx))) / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(y_end, x0 - 1))) * 2 / yDifAvr
DataVal = Cells(y_end, ix + jx)
Else
DistX = (Abs(Cells(y0 - 1, ix) - Cells(y0 - 1, ix + jx))) / xDifAvr
DistY = (Abs(Cells(iy, x0 - 1) - Cells(iy + jy, x0 - 1))) / yDifAvr
DataVal = Cells(iy + jy, ix + jx)
End If
End Select
기본 연산 과정
- DistX : 연산 대상 셀과의 X축 값 편차를 확인, 이후 Scailing
- DistY : 연산 대상 셀과의 Y축 값 편차를 확인, 이후 Scailing
- DataVal : 연산 대상 셀에 입력되어 있는 값
추가로, 아래와 같이 변두리에 있는 셀들은 이웃한 값이 존재하지 않는다.

즉, 연산을 위해 샘플을 모으는 과정에서
1) 최소 값 보다 작은 경우
2) 최대 값 보다 큰 경우
3) 최소 값과 최대 값 사이에 적절히 들어 있는 경우
이 3가지를 고려해야 한다. 여기서 x축과 y축이 독립적으로 작동하므로 총 9가지의 케이스가 나오게 된다.
샘플이 없는 경우에는 가장 마지막 위치에 있는 축 값을 C/O하여 결과 연산에 반영하였다.
이와 같은 처리가 최적화 입장에서 올바른 방법은 아니라 보여지나, 업무의 특성 상 extrapolation을 할 경우가 극히 드물기 때문에 변두리 데이터에 가중치를 주기 위함이다.
구현은 Select Case에 X축, 각각의 Case문 내부에 For문으로 Y축의 경우를 반영한다.
'Distance calculation
Dist = (DistX * DistX + DistY * DistY) ^ 0.5
Call GaussianCalc(Dist, QFac, Resout)
X, Y축을 모두 고려한 최종적인 편차는 2D 면적 상에서의 직선 거리로 연산해 반영 (DistX, DistY -> Dist)
GasussianCalc는 아래와 같이 간단한 코드로 이루어져 있으며, Dist와 Q Factor에 따른 정규 분포 상 결과 값을 계산해 준다.
Sub GaussianCalc(Dist, QFac, Resout)
Dim NExp As Single
Dim Nume As Single
Dim Deno As Single
Const CExp As Single = 2.7818
Const SqRad As Single = 2.5066
NExp = (Dist / (1.414 * QFac)) ^ 2
Nume = CExp ^ -NExp
Deno = QFac * SqRad
Resout = Nume / Deno
End Sub
따라서, ResOut이 최종적으로 나오는 결과 값.
'Gathering result
ResBox(InputTmp, 0) = DataVal
ResBox(InputTmp, 1) = Resout
InputTmp = InputTmp + 1
End If
Next
Next
원하는 것은 샘플의 셀 값과 가중치이므로 모든 샘플에 대한 반복 연산이 끝날 때 까지 배열에 임시로 보관해 둔다.
'Calculating Final result
Nume = 0
Deno = 0
For j = 0 To InputTmp - 1
Nume = Nume + (ResBox(j, 1) * ResBox(j, 0))
Deno = Deno + ResBox(j, 1)
Next
ResFinal = Nume / Deno
연산이 완료 되면 배열 안에 저장 된 데이터를 읽어들이며 샘플 값에 가중치를 곱해 전부 더하고, 여기에 가중치의 총 합을 나누어 주면 최종 결과가 도출된다.
'Applying result
Cells(18 + iy, 0 + ix) = ResFinal
Next
Next
End Sub
도출된 결과를 지정된 셀에 표출한다. Function화 시킬 경우 이 부분은 삭제한다.
<최종 결과>
- Smoothing 적용 전
- Smoothing 적용 후

- Visualization
